《2020年成人高考数学试卷》到底具体内容是什么？下面由我们自成学历信息网小编把收集的内容分享给大家：

一、选择题（本题共12个题，每个题３分，共36分．每个题只有一个选项最符合题意.）

1．2比-3（ ▲ ）.

A．小1 B. 大 -1 C. 小5 D. 大5

2．第二宇宙速度是指物体完全摆脱地球引力束缚,飞离地球所需要的最小初始速度，约为11．2千米／秒，这个数据用科学记数法表示为（ ▲ ）米/秒.

A．1.12×10 B. 11.2×103 C. 1.12 ×104 D. 1.12×103

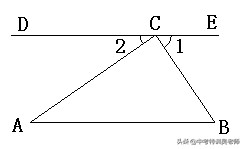
3．如图，直线DE过△ABC顶点C，已知∠1=∠B=56°，∠B=2∠A，则∠2等于（ ▲ ）.

A. 56° B. 28° C. 34° D. 44°

4. 二元一次方程2x+y=7的正整数解有（ ▲ ）.

A．0个 B. 1个 C. 2个 D. 3个

5．下列计算正确的是（ ▲ ）.

A. a+a2=a3 B. (a-b)2=a2-b2 C.2ab2+3b2a=5ab2 D. (ab)2=ab2

6．关于一组数：8，6，4，6，6，下列说法错误的是（ ▲ ）.

A. 平均数为6 B. 众数为6 C. 方差为1.6 D. 中位数为4

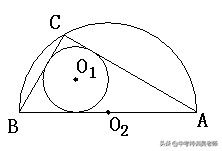
7．如图，⊙和⊙分别是Rt△ABC的内切圆和外接圆，已知∠C是直角，∠A=30°,且⊙的半径为1，则⊙和⊙的圆心距等于（ ▲ ）.

A．√2 B．√3 C．2 √3/3 D．2√2/3

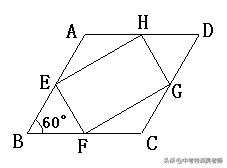
8．如图，菱形ABCD各边中点连线所围成的四边形EFGH的面积为，已知∠A=60°，则菱形周长为（ ▲ ）.

A．8 √3 B． 16 √3 C．8 D．16

9．某服装店租期还剩一个月时购进1000件热销T桖，标价100元，然后九折促销，一个月内刚好卖完，扣除租金等各种开支共6000元后仍获利20%，问每件T桖进价是（ ▲ ）.

A．70 B．72 C．80 D．82

10．已知分式方程

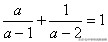
，则关于的不等式的最小整数解是（ ▲ ）.

A．0 B．-1 C．-2 D．2

11．正整数按如下规律排列，比如4在第3行 第1列，按此规律，100在第几行第几列 （ ▲ ）.

A．第13行第8列 B．第14行第8列

C．第14行第9列 D．第15行第10列

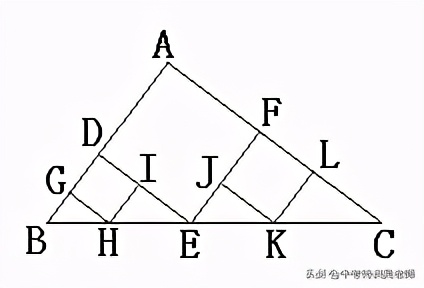
12．如图，在Rt△ABC中，∠A是直角，AB=3，AC=4，分别在Rt△ABC、Rt△DBE、Rt△FEC内作正方形ADEF、正方形DGHI和正方形FJKL，如果顶点H、E、K恰好落在Rt△ABC的斜边BC上，那么DG+FL的值为（ ▲ ）.

A．12/7 B．15/7 C．18/7 D．20/7

二、填空题（本题共6小题，每小题4分，共24分．）

13．计算：

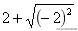
14．已知正多边形的一个内角等于其外角的5倍，则该多边形的边数是 ▲ ．

15．已知

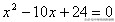
的两根,分别是菱形的两条对角线的长，那么该菱形的面积为 ▲ ．

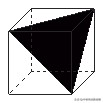
16．如图，阴影三角形是棱长为√2的正方体的截面，则该三角形的面积为 ▲ ．

17．已知A4纸的长、宽分别约为30cm、21cm，现将A4纸矩形ABCD纸片按如图方式折叠，使A与F重合，BE交翻折后的CD于O，则△DOE与△COB的面积之比为 ▲ .

18．如图，点P是反比例函数

上一动点，以P为圆心的圆始终与y轴相切，当⊙P与x轴也相切时，那么⊙P上到原点O距离最近的点的坐标是 ▲ ．

三、解答题(本题共9小题，共90分．请写出必要的解答过程．)

19．（6分）计算：

20．(８分)先化简，再求值：

，其中

21．(8分)为了解某校九年级学生中考体育模拟测试成绩情况，现从中随机抽取部分学生的体育成绩统计如下，其中右侧扇形统计的圆心角α为36°．

体育成绩x（分） 人数（人） 百分比(%)

A等：45≤x≤50 ① ▲ 30

B等：40≤x＜45 12 24

C等：35≤x＜40 8

D等：30≤x＜35 20

E等：25≤x＜30

合计 ② ▲ 100

根据上面提供的信息，回答下列问题：

（1）把表格补充完整：① ▲ ，② ▲ ；

（2）如果30分以下（不含30分）为不合格，需要补考。问本次调查抽取的学生中，需要补考的学生有多少人？

（3）已知该校九年级共有500名学生，如果体育成绩达40分以上（含40分）为优秀，请估计该校九年级学生体育成绩达到优秀的总人数。

22．(10分)如图， AC为堤坝顶部A到地面BC的高度，为测量堤坝高度，在B、D两处分别测得∠ABC=45°，∠ADC=30°，且B、D两处观测点的距离为（4√3 -4）m．

（1）试求堤坝的高度AC；

（2）如果△ABC是堤坝旁车辆通道的横截面形状，一辆2.5吨的厢式货车长为4.2m，宽为1.9m，高为1.8m，问该货车能否通过这个通道？请简要说明理由。

23．(10分）如图，在等腰Rt△ACB中，∠ACB是直角，AC=BC，把一个45°角的顶点放在C处，两边分别与AB交于E、F两点。

（1）将所得△ACE以C为中心，按逆时针方向旋转到△BCG，试求证：△EFC≌△GFC；

（2）若AB=10，AE:BF=3:4，求EF的长

24．（10分）将分别写有3，4，7的三张卡片洗匀后，背面向上放在桌上。现随机抽两张：

（1）请用列表法把所有情况表示出来；

（2）求抽到的两个数字之和为10的概率；

（3）若抽到的两张卡片上的数字分别记为a，b，那么以a，b，2为线段的长，求能围成三角形的概率。

25．（12分）如图，一辆快车从甲地驶往乙地，一辆慢车从乙地驶往甲地，两车同时出发，匀速行驶。设行驶的时间为x（时）两车之间的距离为y（千米），的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系。根据信息，试解答下列问题：

（1）求线段AB所在直线的函数解析式；

（2）求出甲乙两地之间的距离；

（3）已知两车相遇时快车比慢车多行驶40千米，求快车从甲地到达乙地所需的时间t的值；并求此时慢车距甲地的距离。

26．（12分）如图，P，Q分别是等边△ABC的AB和AC边延长线上的两动点，点P由B向A匀速移动，同时点Q以相同的速度由C向AC延长线方向移动，

连接PQ交BC边于点D，M为AC中点，连接PM，已知AB=6。

（1）若点P，Q的速度均为每秒1个单位，设点P运动时间为x，△APM的面积为y，试求出关于的函数关系式；

（2）当时间x为何值时，△APM为直角三角形；

（3）当时间x为何值时，△PQM面积最大？并求此时y的值。

27．（14分）如图，一次函数

分别交x轴、y轴于A、B两点，抛物线

过A、B两点．

（1）求这个抛物线的解析式；

（2）作垂直x轴的直线，在第一象限交直线AB于M，交这个抛物线于N。求当 取何值时，MN有最大值？最大值是多少？

（3）在（2）的情况下，以A、M、N、D为顶点作平行四边形，求第四个顶点D的坐标．

点击显示全文

以上就是自成学历信息网为您收集的有关《2020年成人高考数学试卷》的全部内容，希望能给您带来帮助，想要了解更多成考自考相关信息，可持续关注自成学历信息网(www.zc77.cn)。